A digit íze

Digitalizálás inkább hangos módra, „azmiaz hogy digitális”-ról való gondolatok, avagy:

Mérjük meg a tengert!

A digitális világ első közelítésben a számokról szól.  Történetileg is úgy alakult, hogy eleinte azok életét alakította át a számítógép megjelenése, terjedése akik már eleve számoszlopok, kockás papírok közt élték mindennapjaikat: raktárosok, bérszámfejtők, pénzügyérek, tüzérségi lőelem kalkuláló brigádok, ipari és egészségügyi laborok munkatársai barátkoztak elsőként a monitor, billentyűzet, adathordozó szentháromsággal a napi kenyérharc során.  Mindazok tehát, akik már ezt megelőzően is kártyákon, kartonokon, táblázatokba rendezett számtengerek között élték életüket, végeztek matematikai műveleteket papíron ceruzával, abakusszal, elmés mechanikus fogaskerekes tekerős összeadógépekkel vagy csilingelő pénztárgépekkel.

Olyan dolgokkal foglalkoznak ők, amik ábrázolható számértékkel, fizikai mennyiségként jelennek meg a mi hétköznapi valóságunkban is: a vérsüllyedés milliméterben, a termék típus- és darabszáma, pénznem és százalék, vagy az oldalszél sebessége, meg az ágyúcső hőmérséklete.  És amivel a földi halandók úgy egyébként foglalkoznak úgy mint mozdulatok, tánc, zene, érzékek, költészet, álló vagy mozgó alakok, festmények, formák, nos azok mind olyan objektumok amiről úgy elsőre nem a számok rendezett tengere jut az ember eszébe.  Hogyan kerül ez be a számítógépbe, hogyan digitalizálódik, hogyan lehet számokra váltani mondjuk a honvágy vagy az irigység érzetét?  Hát azt hiszem sehogy.  De azt itt, most megmutatom, hogy ez a szép új digitális világ hogyan is próbálkozik megszoborni ezt a fából vaskarikát.

Ami a moziban a szemünk elé kerül az fény(kép) és hang, azaz fizikai értelemben különféle hullámok, rezgések összessége.  Ha megkérek valakit, hogy rajzoljon egy hullámot, akkor egy olyan vonal kerül a papírra ami leginkább egy szaladó kígyó felülnézeti képére, vagy a vízfelszín oldalnézeti metszetére hasonlít leginkább.  Azt kell éreznünk, hogy ennek a hullám dolognak az időhöz van nagyon sok köze.  Valaminek a változása, aminek a pillanatnyi állapotát merevítettük ki a rajzon, mint egy fényképen, abban az adott pillanatban.  Legyen első példánk a hang amiről tudjuk, hogy rezgés.  Amolyan hullámszerű dolog, amivel nap mint nap szembesülünk: a pendülő húr, a dob, a hangszóró membránja, a rezdülő ádámcsutka érintésével ez mindenkinek napi tapasztalat.  Az ad hangot ami rezeg.  A rezgés pedig hullámként terjed tova.  A hullám természete pedig a víz felszínén látszik a legjobban.  Alakítsuk hát számokká azaz digitalizáljuk a tenger hullámzását.

Áll egy stég a Nagy Víz homokos partjánál.  A stégről egy létra vagy lépcsőféleség erszkedik a mélybe, le egészen az iszapos fenékig.  A stégen ül egy Pillanó és azt nézi, hogy alulról számítva vajon éppen a hányadik lépcsőfokot nyaldossa a víz.  Azaz hány lépcsőfoknyi az adott pillanatban a víz pillanatnyi magassága?  Mi a képen ezt úgy látjuk, hogy a lépcsőfokok közötti lyukakból hány kékül be az ábrán.  A Pillanó egy fürge jószág, így a kezében tartott formanyomtatványra másodpercenként mondjuk tízszer feljegyzi a  frissen öblített lépcső sorszámát.  Ha jól csinálja, akkor ezzel számokká alakította a hullámzást, a papíron ott van rendezett számtengerként a hullámzás formája. 

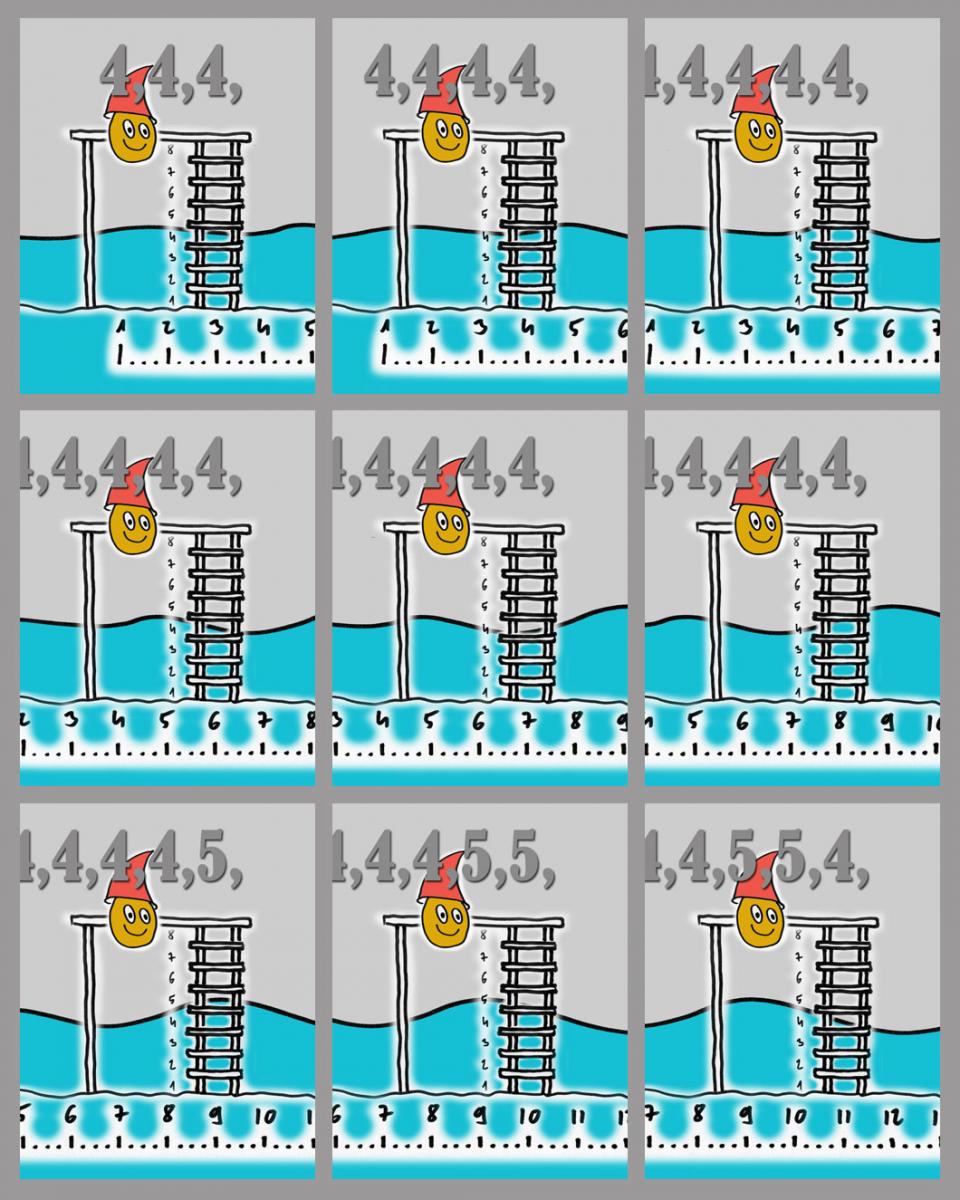
Nézzük csak: eleinte nyugodt a tenger, Pillanó nagy nyugalommal írogatja a lapra 4-4-4-4-5-4.  Itt már látszik az analóg és a digitális világ közötti egyik alapvető különbség.  Figyeljük meg hogy a keletkezett számok sorában semmi nem utal arra, hogy a két lépcsőfok közti szintkülönbséget mennyire tölti ki a víz.  Egyformán négyes osztályzatot kap a félig tele, az éppen-hogy elérte és a majdnem az ötöst áztatja szint is.  A sorban egymást követő egyforma számértékek magát a digitális csendet jelentik.  De ez nem marad így, kicsit odébb elsuhan egy hajó és jönnek a hullámok. 

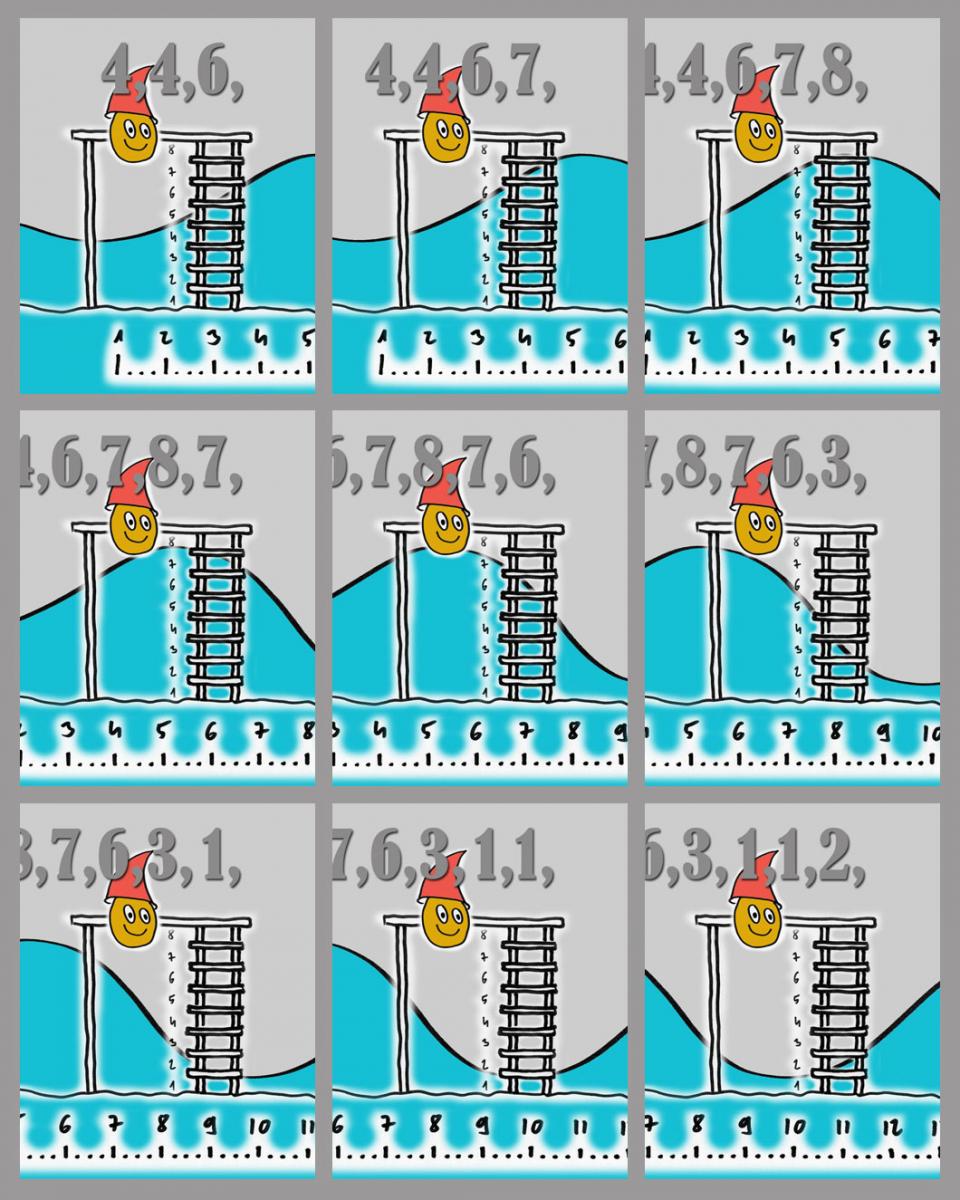
Most már a létra összes fokát áztatja a víz, 8 és 1 között a hullám nagyságával arányosan keletkezik a számok sora.   Itt most mi numerizáltuk a hullám alakját, ez már számok rendezett csomagja.  Innen már csak egy ugrás, hogy a tízes számrendszer számait átfejtsük a kettes számrendszer pötty/nem pötty, lyukas/nemlyukas, ég-a-lámpa/nem-ég-a-lámpa vagyis a digitális világ igen/nem jeleivé, amit azután spirális barázdákba rendezve belelyuggathatunk a cd korong felületébe.  És ezzel a kettes számrendszerbe való átalakítással léptünk be a DI-gitális, a kétállapotú világba, az analóg világ egy részletét DI-gitalizáltuk, elvégeztük az analóg-digitális-, azaz az AD-konverziót.

Jöjjenek akkor az apró-betűs megjegyzések.  Az analóg digitális átalakításkor az elején két nagyon fontos elhatározást kell tennünk. 

1.) Milyen pontossággal akarjuk követni a vízállás magasságát azaz hány foka legyen a létrának?  Másképp fogalmazva hány sávra osztjuk a legkisebb és legnagyobb várható vízmagasság közti távolságot? 

2.) Milyen időközönként írjuk fel az értéket, vagyis milyen gyakorisággal mérünk?  Ez két olyan döntés aminek nagyon sok következménye lesz. Lássuk tehát ezeket a következményeket:  

A létrafokok száma.  Szélcsend idején ha arra is kíváncsiak vagyunk milyen a kicsi hullámzás, akkor finomabb létrára, sokkal több létrafokra van szükségünk.  A távolság durva felosztása nem képes követni a kismértékű szintváltozásokat.  Ezt mutatja az egymást követő sok egyforma 4-es az ábrán, van már valami enyhe hullámzás de ez nem látszik a digitalizált adatfolyamban. 

Mi az imént a stég alatt „véletlenül” 8 szintre osztottuk a magasságot.  Ez a digitális nullák és egyesek  világában 3 biten jeleníthető meg, ami azt jelenti, hogy a kettes számrendszerben nyolc egymástól elkülönülő szintet olyan számmal tudok leírni ami három helyiérték széles, három számjegyű szám:

0 = 000 = o o o = • • • 

1 = 001 = o o • = — — •

2 = 010 = o • o = — • —

3 = 011 = o • • = • — —

4 = 100 = • o o = — • •

5 = 101 = • o • = — • —

6 = 110 = • • o = — — •

7 = 111 = • • • = — — —

Ezért használjuk a kettes számrendszert, mert ebben csak két „valami” kell az értékek megjelenítéséhez.  Van lyuk a lemezen vagy nincs, rövid pöttyöt égetett a lézer a felületre vagy hosszút.  Ezt próbáltam ábrázolni a táblázatban: az egyik rendszerben egyest jelez a fekete pötty egy másikban, amit a sorban az utolsó egyenlőségjel utáni írásmóddal mutatok, pedig a nullát.  Ez megegyezés kérdése, szabványban rögzítik és működhet mind a kettő.  De ilyen és hasonló megegyezések miatt kerül azután „pluszos” és „mínuszos” DVD a boltokba, amit vagy fölismer a meghajtó vagy nem.  De térjünk vissza a hullámábrázolás finomításához.  Ha nem találjuk elégnek a nyolc szintű megfigyelést, a következő lépcső a négy helyiértéken történő ábrázolás.  A négyjegyű kettes számrendszerbeli szám már tizenhat szintet különböztet meg, azaz tizenhat lépcsőfok vezet fel a stégre, de ekkor mérésenként már négy jelet kell pöttyinteni az adathordozóra.  Ez két problémát vet föl: több hely kell a tároláshoz és az ugyanannyi rendelkezésre álló idő miatt/alatt gyorsabban kell rajzolni a pöttyöket.  Több tárhely és nagyobb teljesítmény kell hozzá. 

A gyakoriság.  A másik nagyon fontos elhatározás amit meg kell tennünk az analóg digitális átalakítás elején az a mintavételek gyakoriságával kapcsolatos.  Ha arra kérjük a Pillanót, hogy ne szaporázza annyira, nem akarunk mi annyi szám között bogarászni, elég csak minden tizedik órajelre mérni, az ábrán mondjuk egynél és tíznél (a vonalzó számai alul), akkor lazán lemaradunk az ötnél látható hullámhegyről.  A digitális adat szerint nem erősebb a hullámzás a négyes szintnél.  Ritka mintavételezésnél nem tudjuk nyomon követni a két mintavétel közötti gyors változásokat.

A túlvezérlés. Egy harmadik probléma, a cunami eset:

Nagyon gondosan kell arra ügyelni, hogy ne jussanak túl nagy hullámok az analóg-digitál átalakítóra.  Ha ugyanis meghaladja az ábrázolható legmagasabb értéket a beérkező hullám, akkor a Pillanó (feltéve hogy tud úszni, vagy jó erősen kapaszkodni és a szuszogás problémát is menedzseli valahogy) nem tud mást tenni mint írja a maximális 8-as értéket rendületlenül, miközben ő is, mi is tudjuk, hogy a hullám taraja messze ez érték fölött van.  Nos ennek az lesz az eredménye, hogy a digitális adatban nem lesz meg a hullám szép gömbölyded teteje, hanem olyan alakja lesz mintha egy nagy sárga Caterpillar simára, vízszintesre dózerolta volna a dombtetőt a bitek engedte legmagasabb szinten.  Ha ez a hullám hang, akkor borzalmasan torz lesz.  Ilyen hiba után hiába halkítjuk le a jelet az már helyreállíthatatlan, halkan lesz torz, ugyanis nincs információnk arról, hogy milyen volt a hullám alakja a stég fölött.  Annak eredeti alakját már nem tudjuk helyreállítani a számtengerből. 

Összefoglalva mi az hogy digitális?

Amikor a hullámot digitális jellé alakítottuk akkor azt tettük, hogy bizonyos időközönként bizonyos pontossággal ránéztünk, hogy mekkora az értéke. Az előbb említett „bizonyos időközönként“ lesz a mintavétel gyakorisága a mintavételi frekvencia,  más néven órajel, a „bizonyos pontossággal“ pedig a bitmélység.  A digitális jelnél tehát csak azt tudom, hogy az adott pillanatban éppen melyik sávba, példánkban melyik lépcsőfokok közé esett a nagysága.  Azt, hogy a két mérés között mit csinált arról fogalmam nincs.  Arra csak következtetni tudok: ha az egyik időpontban ekkora a következőnél meg akkora akkor a két mérési időpont közt is a két mért érték között lehetett valahol...  Mint a villanypóznák és a földfelszín.  Ha a póznák tetejét egyenesekkel összekötöm, úgy nagyjából kiadódik a domborzat formája.  De a két pózna közti téglarakás vagy az árok már nem látszik.  És ugyanígy a mért jelnagyság is csak bizonyos pontossággal állítható helyre.  Csak azt tudjuk, hogy elérte a lépcső szintjét, hogy mennyivel haladta meg, azt nem tudjuk meg a digitális adatból.   

Az analóg világnál ha vizsgálok egy jelenséget, mindig van egy még közelebbi szint.  Ha a digitális fényképet nagyítom, akkor eljutok oda, hogy egy elemi adat, egy pixel, egy homogén egyszínű mintavételi egység tölti be a képernyőmet.  Hiába nagyítom tovább nem kapok plusz információt.  Ha ahhoz az analóg dologhoz közelítünk amiről a kép készült, akkor újabb univerzumok nyílnak előttünk, makrovilág, sejtszint, és csak a molekuláris, atomi szinten kezd hasonlítani a digitálisra ez az analóg, való világ.  Legalábbis a fizikusok szerint most még így gondoljuk...

Tehát az analóg folytonos, a digitális szaggatott, pixeles, diszkrét különálló elemekből áll össze és csak bizonyos távolságból látszik folytonos egésznek.